FUNCIÓN AFÍN, CONSTANTE Y LÍNEAL

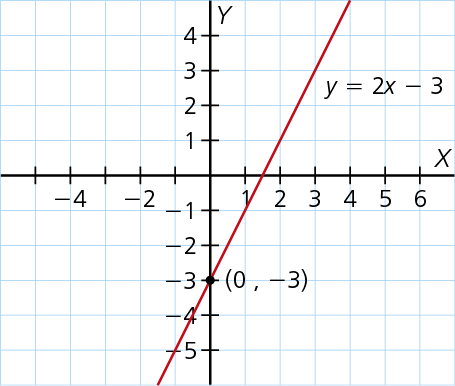
Una función afín es aquella cuya expresión algebraica de la forma y=mx+n.

• El dominio de las funciones afines es el conjunto de los números reales D(f)=R.
• El recorrido es también el conjunto de los números reales, D(f)=R.
• La representación gráfica de una función afín es una recta que cumple las siguientes condiciones: 

1. El coeficiente de x, m, es la pendiente de la recta.  
2. El número n es la ordenada en el origen, es decir, la coordenada y del punto de corte de la recta con el eje Y. Así, la recta pasa por el punto (0, n). 
3. Si la pendiente es positiva (m>0) la función es creciente, y si la pendiente es negativa (m<0), la función es decreciente. 

 

Si n=0 en la expresión general de la función afín, y=mx+n, entonces la función recibe la denominación de líneal, mientras que si m=0, se trata de una función constante.

 Una función líneal o de proporcional directa, es aquella cuya expresión algebraica es de la forma y=f(x)=mx, con m distinto de 0.  

• El dominio de todas las funciones líneales es el conjunto de los números reales, D(f)=R, pues para cualquier número real, x, siempre se puede hallar su imagen, y, multiplicando al número x por m. 
• El recorrido es, igualmente, el conjunto de los números reales, D(f)=R, dado que para cada valor de la función, y, siempre se puede obtener su valor de x asociado, dividiendo el valor de y entre m. 
• La representación gráfica de una función líneal es una recta que pasa por el origen de coorenadas y que tiene las siguientes características:

1.  El coeficiente de x, m, es la pendiente de la recta e indica la inclinación que tiene la recta con respecto al eje de abcisas, X. 
2.  Si la pendiente es positiva (m>0), la función es creciente, y si la pendiente es negativa (m<0), la función es decreciente.

Las funciones líneales reciben el nombre de proporcionalidad directa, pues la variable independiente, x, y la variable dependiente, y, son magnitudes directamente proporcionales.

La pendiente, m, es la constante de proporcionalidad: m=y/x.