FUNCIÓN CUADRÁTICA

Una función cuadrática es una función polinómica de segundo grado.           

Su expresión algebraica es :                                                                                                                                  

                                                         f (x) = ax2 + bx + c                                                  

Las letras a, b y c son números reales.  

Su dominio son todos los números reales:

                                                                             D (f) = IR                                                                 

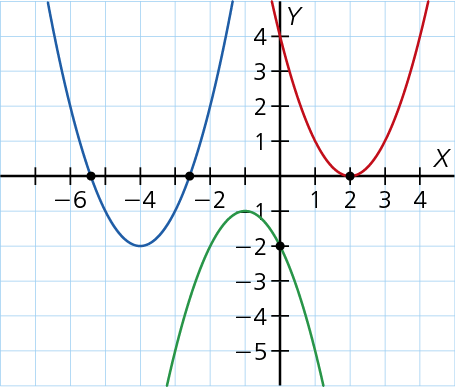
• Su representación gráfica es una parábola, donde si a es mayor que 0, las ramas de la parábola apuntan hacia arriba y es convexa; Si a es menor que 0 las ramas apuntan hacia abajo y es cóncava.            El vértice de la parábola de la función es el mínimo absoluto si a > 0 y el máximo absoluto , si a < 0. Sus coordenadas son:

V=(xv ,yv)→xv=-b/2a ,yv=f(-b/2a)

• La parábola es simétrica respecto de una recta paralela al eje Y que pasa por el vértice, llamada eje de simetría de la parábola, y de ecuación x=-b/2a
• La función es creciente a un lado del eje de simetría y decreciente en el otro.
• Los puntos de corte de la parábola con los ejes de coordenadas son:

- Con el eje X: y=0→ax2+bx+c=0

- Con el eje Y: x=0,→y=f(0)=c. Luego el único punto de corte es el (0,c)

FUNCIÓN EXPONENCIAL

Una función exponencial es aquella cuya expresión algebraica es de la forma f (x)=ax, donde a>0 y a es distinto de 1.

Características:

- Es continua en su dominio, que es D (f)= R. Su recorrido es (0,+ infinito).

- Pasa por el punto (0,1) pues f (0)= a elevado a la 0= 1, y por el punto (1,a) ya que f(1)=a elevado a la 1=a.

- Corta al eje Y en el punto (0,1) y no tiene puntos de corte con el eje X.

- El eje X es una asíntota horizontal: si a > 1, a medida que los valores  de x decrecen, la función se acerca a la recta y=0, y si 0 <a<1, la función es decreciente.

Si a >1

 Si 0<a<1

- Dos de las funcines exponenciales más importantes son la función expnencial cuya base es el número e, f (x)= e elevado a la x, y la función exponencial en base 10, f (x) = 10.

FUNCIÓN DEFINIDA A TROZOS

Una función definida a trozos es una función que tiene distintas expresiones algebraicas según los valores que toma la variable x. 

FUNCIÓN AFÍN, CONSTANTE Y LÍNEAL

Una función afín es aquella cuya expresión algebraica de la forma y=mx+n.

• El dominio de las funciones afines es el conjunto de los números reales D(f)=R.
• El recorrido es también el conjunto de los números reales, D(f)=R.
• La representación gráfica de una función afín es una recta que cumple las siguientes condiciones: 

1. El coeficiente de x, m, es la pendiente de la recta.  
2. El número n es la ordenada en el origen, es decir, la coordenada y del punto de corte de la recta con el eje Y. Así, la recta pasa por el punto (0, n). 
3. Si la pendiente es positiva (m>0) la función es creciente, y si la pendiente es negativa (m<0), la función es decreciente. 

 

Si n=0 en la expresión general de la función afín, y=mx+n, entonces la función recibe la denominación de líneal, mientras que si m=0, se trata de una función constante.

 Una función líneal o de proporcional directa, es aquella cuya expresión algebraica es de la forma y=f(x)=mx, con m distinto de 0.  

• El dominio de todas las funciones líneales es el conjunto de los números reales, D(f)=R, pues para cualquier número real, x, siempre se puede hallar su imagen, y, multiplicando al número x por m. 
• El recorrido es, igualmente, el conjunto de los números reales, D(f)=R, dado que para cada valor de la función, y, siempre se puede obtener su valor de x asociado, dividiendo el valor de y entre m. 
• La representación gráfica de una función líneal es una recta que pasa por el origen de coorenadas y que tiene las siguientes características:

1.  El coeficiente de x, m, es la pendiente de la recta e indica la inclinación que tiene la recta con respecto al eje de abcisas, X. 
2.  Si la pendiente es positiva (m>0), la función es creciente, y si la pendiente es negativa (m<0), la función es decreciente.

Las funciones líneales reciben el nombre de proporcionalidad directa, pues la variable independiente, x, y la variable dependiente, y, son magnitudes directamente proporcionales.

La pendiente, m, es la constante de proporcionalidad: m=y/x.

BIENVENIDOS, BENVINGUTS, ETORRI, BENVIDO

En este blog os introduciremos al mundo de las funciones. Somos un grupo de alumnos de 4º  de ESO que aspiran a sacar un 10 en este trabajo gracias a este blog. Así que esperamos que aprendáis con nuestros posts de la misma manera que nosotros lo hicimos escribiéndolos.